Section03 Cramer's Rule, Inverses, and Volumes

Cramer's Rule

KEY IDEA

$$\begin{array}{c} \boldsymbol{A}\boldsymbol{x} = \boldsymbol{b} \\ \\ \big\Downarrow \\ \\ \boldsymbol{A} \left[ \begin{matrix} x_{1} & 0 & 0 & \cdots & 0 \\ x_{2} & 1 & 0 & \cdots & 0 \\ x_{3} & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{n} & 0 & 0 & \cdots & 1 \\ \end{matrix} \right] = \left[ \begin{matrix} \boldsymbol{b} & \boldsymbol{a}_{\boldsymbol{\cdot}2} & \boldsymbol{a}_{\boldsymbol{\cdot}3} & \cdots & \boldsymbol{a}_{\boldsymbol{\cdot}n} \end{matrix} \right]= \boldsymbol{B}_{1}\\ \\ \boldsymbol{A} \left[ \begin{matrix} 1 & x_{1} & 0 & \cdots & 0 \\ 0 & x_{2} & 0 & \cdots & 0 \\ 0 & x_{3} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & x_{n} & 0 & \cdots & 1 \\ \end{matrix} \right] = \left[ \begin{matrix} \boldsymbol{a}_{\boldsymbol{\cdot}1} & \boldsymbol{b} & \boldsymbol{a}_{\boldsymbol{\cdot}3} & \cdots & \boldsymbol{a}_{\boldsymbol{\cdot}n} \end{matrix} \right]= \boldsymbol{B}_{2}\\ \\ \big\Downarrow \\ \\ \det(\boldsymbol{A} \left[ \begin{matrix} x_{1} & 0 & 0 & \cdots & 0 \\ x_{2} & 1 & 0 & \cdots & 0 \\ x_{3} & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{n} & 0 & 0 & \cdots & 1 \\ \end{matrix} \right]) = (\det \boldsymbol{A})(x_{1} \det{ \left[ \begin{matrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{matrix} \right]}) = \det \boldsymbol{B}_{1} \\ \\ \det(\boldsymbol{A} \left[ \begin{matrix} 1 & x_{1} & 0 & \cdots & 0 \\ 0 & x_{2} & 0 & \cdots & 0 \\ 0 & x_{3} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & x_{n} & 0 & \cdots & 1 \\ \end{matrix} \right]) = (\det \boldsymbol{A})(x_{2}\det \left[ \begin{matrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{matrix} \right]) = \det {\boldsymbol{B}_{2}}\\ \\ \big\Downarrow \\ \\ x_{1}(\det \boldsymbol{A}) = \det \boldsymbol{B}_{1} \\ x_{2}(\det \boldsymbol{A}) = \det \boldsymbol{B}_{2} \\ \\ \big\Downarrow \\ \\ x_{1} = \frac{\det \boldsymbol{B}_{1}}{\det \boldsymbol{A}} \\ x_{2} = \frac{\det \boldsymbol{B}_{2}}{\det \boldsymbol{A}} \\ \end{array}$$

Defination

• If $\det {\boldsymbol{A}}$ is not zero, $\boldsymbol{Ax} = \boldsymbol{b}$ is solved by determinants: $$\begin{matrix} x_{1} = \frac{\det{\boldsymbol{B}_{1}}}{\det {\boldsymbol{A}}} & x_{2} = \frac{\det{\boldsymbol{B}_{2}}}{\det {\boldsymbol{A}}} & \cdots & x_{n} = \frac{\det{\boldsymbol{B}_{n}}}{\det {\boldsymbol{A}}} \end{matrix}$$

  • The matrix $\boldsymbol{B}_{j}$ has the $j$th column of $\boldsymbol{A}$ replaced by the vector $\boldsymbol{b}$.

    $$\boldsymbol{B}_{j} = \left[ \begin{matrix} \boldsymbol{a}_{\boldsymbol{\cdot}1} & \boldsymbol{a}_{\boldsymbol{\cdot}2} & \cdots & \boldsymbol{a}_{\boldsymbol{\cdot} j-1} & \boldsymbol{b} & \boldsymbol{a}_{\boldsymbol{\cdot} j+1} & \cdots & \boldsymbol{a}_{\boldsymbol{\cdot}n} \end{matrix} \right]$$

Properties

• Inefficient

Applying to inverse matrix

$$\begin{array}{c} \boldsymbol{AA}^{-1} = \boldsymbol{I} \\ \\ \big\Downarrow \\ \\ \boldsymbol{A}(\boldsymbol{A}^{-1})_{\boldsymbol{\cdot}j} = \left[ \begin{matrix} 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{matrix} \right] \\ \\ \big\Downarrow \\ \\ (\boldsymbol{A}^{-1})_{ij} = \frac{\det{\boldsymbol{B}_{i}}}{\det{\boldsymbol{A}}} \\ \boldsymbol{B}_{i} = \left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1(i-1)} & 0 & a_{1(i+1)} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2(i-1)} & 0 & a_{2(i+1)} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{(j-1)1} & a_{(j-1)2} & \cdots & a_{(j-1)(i-1)} & 0 & a_{(j-1)(i+1)} & \cdots & a_{(j-1)n} \\ a_{j1} & a_{j2} & \cdots & a_{j(i-1)} & 1 & a_{j(i+1)} & \cdots & a_{jn} \\ a_{(j+1)1} & a_{(j+1)2} & \cdots & a_{(j+1)(i-1)} & 0 & a_{(j+1)(i+1)} & \cdots & a_{(j+1)n} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{n(i-1)} & 1 & a_{n(i+1)} & \cdots & a_{nn} \\ \end{matrix} \right] \\ \\ \big\Downarrow \\ \\ \det{\boldsymbol{B}_{i}} = C_{ji} \\ (\boldsymbol{A}^{-1})_{ij} = \frac{\det {\boldsymbol{B}_{i}}}{\det \boldsymbol{A}} = \frac{C_{ji}}{\det {\boldsymbol{A}}} \\ \\ \big\Downarrow \\ \\ \color{#D0104C}{\boldsymbol{A}^{-1} = \frac{1}{\det \boldsymbol{A}}\boldsymbol{C}^{\text{T}}} \end{array}$$

• $\boldsymbol{C} \Rightarrow$ Cofactor Matrix

• direct proof $$\left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{matrix} \right] \left[ \begin{matrix} C_{11} & C_{21} & C_{31} \\ C_{12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \\ \end{matrix} \right] = \left[ \begin{matrix} \det{\boldsymbol{A}} & 0 & 0 \\ 0 & \det{\boldsymbol{A}} & 0 \\ 0 & 0 & \det{\boldsymbol{A}} \\ \end{matrix} \right] = (\det \boldsymbol{A})\boldsymbol{I}$$

• How to understand $a_{21}C_{11} + a_{22}C_{12} + a_{23}C_{13} = 0$?
  • $a_{21}C_{11} + a_{22}C_{12} + a_{23}C_{13}$ is the determinant of a new matrix whose first row is replaced by the second row. Therefore, it's zero.

Area of a Triangle

• The triangle with corners $(x_{1}, y_{1})$, $(x_{2}, y_{2})$, $(x_{3}, y_{3})$ $$\frac{1}{2} \left\vert \begin{matrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{matrix} \right\vert$$
• A parallelogram starting from $(0,0)$ has area = $2$ by $2$ determinant.
  • The area of parallelogram has the same properties as determinants:
    1. When $\boldsymbol{A} = \boldsymbol{I}$, the parallelogram becomes the unit square.
    2. When rows are exchanged, the determinant reverses sign. The absolute value stays the same.
    3. The area is also a linear function of each row seperately.

The Cross Product

Defination 01

$$\begin{array}{c} \boldsymbol{u} = (u_{1}, u_{2}, u_{3}); \boldsymbol{v} = (v_{1}, v_{2}, v_{3}) \\ \boldsymbol{u} \times \boldsymbol{v} = \left\vert \begin{matrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \\ \end{matrix} \right\vert = (u_{2}v_{3} - u_{3}v_{2})\boldsymbol{i} + (u_{3}v_{1} - u_{1}v_{3})\boldsymbol{j} + (u_{1}v_{2} - u_{2}v_{1})\boldsymbol{k}\\ \boldsymbol{i} = \left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right] \boldsymbol{j} = \left[ \begin{matrix} 0 \\ 1 \\ 0 \end{matrix} \right] \boldsymbol{k} = \left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] \end{array}$$

Defination 02

The cross product is a vector with length $\Vert \boldsymbol{u} \Vert \Vert \boldsymbol{v} \Vert \vert sin \theta \vert$. Its direction is perpendicular to $\boldsymbol{u}$ and $\boldsymbol{v}$. It points "up" or "down" by the right hand rule.

Properties

1. $\boldsymbol{u} \times \boldsymbol{v} = -(\boldsymbol{v}\times \boldsymbol{u})$ (row exchange make sign change.)
2. $\boldsymbol{u} \times \boldsymbol{v} \perp \boldsymbol{u}$ and $\boldsymbol{u} \times \boldsymbol{v} \perp \boldsymbol{v}$ ($\boldsymbol{u}\cdot(\boldsymbol{u} \times \boldsymbol{v}) = \boldsymbol{v}\cdot(\boldsymbol{u} \times \boldsymbol{v}) = 0$)
3. The cross product of any vector with itself (two equal rows) is $\boldsymbol{u}\times \boldsymbol{u} = \boldsymbol{0}$.
4. The length of $\boldsymbol{u} \times \boldsymbol{v}$ is the area of parallelogram sides $\boldsymbol{u}$ and $\boldsymbol{v}$.

Direction

• $\boldsymbol{u} \times \boldsymbol{v}$ points along your right thumb when the fingers curl from $\boldsymbol{u}$ to $\boldsymbol{v}$.

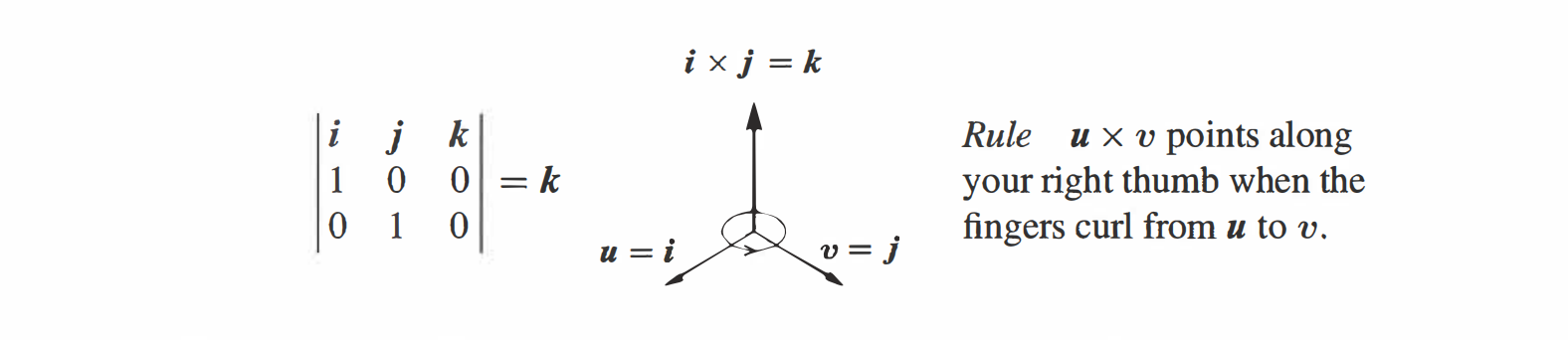
Triple Product = Determinants = Volumes

• Triple product $$\begin{array}{ll} (\boldsymbol{u} \times \boldsymbol{v}) \cdot \boldsymbol{w} = \left[ \begin{matrix} \left\vert \begin{matrix} u_{2} & u_{3} \\ v_{2} & v_{3} \end{matrix} \right\vert \\ -\left\vert \begin{matrix} u_{1} & u_{3} \\ v_{1} & v_{3} \end{matrix} \right\vert \\ \left\vert \begin{matrix} u_{1} & u_{2} \\ v_{1} & v_{2} \end{matrix} \right\vert \\ \end{matrix} \right] \cdot \left[ \begin{matrix} w_{1} \\ w_{2} \\ w_{3} \end{matrix} \right] = w_{1} \left\vert \begin{matrix} u_{2} & u_{3} \\ v_{2} & v_{3} \end{matrix} \right\vert - w_{2} \left\vert \begin{matrix} u_{1} & u_{3} \\ v_{1} & v_{3} \end{matrix} \right\vert + w_{3} \left\vert \begin{matrix} u_{1} & u_{2} \\ v_{1} & v_{2} \end{matrix} \right\vert \\ = \left\vert \begin{matrix} w_{1} & w_{2} & w_{3} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{matrix} \right\vert = \left\vert \begin{matrix} u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \\ w_{1} & w_{2} & w_{3} \end{matrix} \right\vert \end{array}$$

Nullspace and cofactor matrix

• If $\boldsymbol{A}$ is singular $$\begin{array}{ll} \because & \boldsymbol{AC}^{\text{T}} = (\det \boldsymbol{A})\boldsymbol{I} \text{ and } \boldsymbol{A} \text{ is singular.}\\ \therefore & \boldsymbol{AC}^{\text{T}} = \boldsymbol{0} \\ \therefore & \text{The columns of } \boldsymbol{C}^{\text{T}} \text{ is contained in the nullspace of } \boldsymbol{A} \\ \therefore & \text{The cofactors along the row is contained in the nullspace, when } \boldsymbol{A} \text{ is singular.}\\ \end{array}$$

Polar Coordinates

2D

$$\begin{array}{c} x = r\cdot \cos\theta; y = r\cdot \sin\theta \\ \\ \boldsymbol{J} = \left[ \begin{matrix} \frac{\partial{x}}{\partial{r}} & \frac{\partial{x}}{\partial{\theta}} \\ \frac{\partial{y}}{\partial{r}} & \frac{\partial{y}}{\partial{\theta}} \\ \end{matrix} \right] = \left[ \begin{matrix} \cos \theta & -r \cdot \sin\theta \\ \sin \theta & r \cdot \cos\theta \end{matrix} \right] \\ \\ \text{Each cols of } \boldsymbol{J} \text{ are orthonal to each other.} \\ \det \boldsymbol{J} = r \end{array}$$

3D

$$\begin{array}{c} x = \rho \sin\phi\cos\theta; y = \rho \sin\phi\sin\theta; z = \rho\cos\phi \\ \\ \boldsymbol{J} = \left[ \begin{matrix} \frac{\partial{x}}{\partial{r}} & \frac{x}{\partial{\phi}}& \frac{\partial{x}}{\partial{\theta}} \\ \frac{\partial{y}}{\partial{r}} & \frac{y}{\partial{\phi}}& \frac{\partial{y}}{\partial{\theta}} \\ \frac{\partial{z}}{\partial{r}} & \frac{z}{\partial{\phi}}& \frac{\partial{z}}{\partial{\theta}} \\ \end{matrix} \right] = \left[ \begin{matrix} \sin\phi\cos\theta & \rho\cos\phi\cos\theta & -\rho\sin\phi\sin\theta \\ \sin\phi\sin\theta & \rho\cos\phi\sin\theta & \rho\sin\phi\cos\theta \\ \cos\phi & -\rho\sin\phi & 0 \\ \end{matrix} \right] \\\\ \text{Each cols of } \boldsymbol{J} \text{ are orthonal to each other.} \\ \det \boldsymbol{J} = \rho \end{array}$$

Properties from Exercises

1. Another perspective of Cramber's rule. $$\begin{array}{ll} & \text{Suppose } \boldsymbol{A} = \left[ \begin{matrix} \boldsymbol{a}_{1} & \boldsymbol{a}_{2} & \boldsymbol{a}_{3} \end{matrix} \right] \\ \because & \boldsymbol{Ax} = \boldsymbol{b} \\ \therefore & \boldsymbol{b} = \boldsymbol{a}_{1}x_{1} + \boldsymbol{a}_{2}x_{2} + \boldsymbol{a}_{3}x_{3} \\ \therefore & \left\vert \begin{matrix} \boldsymbol{b} & \boldsymbol{a}_{2} & \boldsymbol{a}_{3} \end{matrix} \right\vert = \left\vert \begin{matrix} \boldsymbol{a}_{1}x_{1} + \boldsymbol{a}_{2}x_{2} + \boldsymbol{a}_{3}x_{3} & \boldsymbol{a}_{2} & \boldsymbol{a}_{3} \end{matrix} \right\vert\\ & = x_{1} \left\vert \begin{matrix} \boldsymbol{a}_{1} & \boldsymbol{a}_{2} & \boldsymbol{a}_{3} \end{matrix} \right\vert = x_{1}(\det \boldsymbol{A}) \end{array}$$
2. $\boldsymbol{A}\boldsymbol{C}^{\text{T}} = \left[ \begin{matrix} \det \boldsymbol{A} & 0 & \cdots & 0 \\ 0 & \det \boldsymbol{A} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \det \boldsymbol{A} \end{matrix} \right]= (\det \boldsymbol{A})\boldsymbol{I}$
3. $\boldsymbol{A} = (\det \boldsymbol{A})(\boldsymbol{C}^{\text{T}})^{-1}$
4. $\boldsymbol{A}\boldsymbol{C}^{\text{T}} = (\det \boldsymbol{A})\boldsymbol{I} \Rightarrow (\det \boldsymbol{AC}^{\text{T}}) = (\det (\det \boldsymbol{A})\boldsymbol{I}) \Rightarrow (\det \boldsymbol{A})(\det \boldsymbol{C}) = (\det \boldsymbol{A})^{n} \\ \Rightarrow \color{#D0104C}{\det \boldsymbol{C} = (\det \boldsymbol{A})^{n-1}}$
5. When $\boldsymbol{A}$ and $\boldsymbol{A}^{-1}$ are intergers, $\det\boldsymbol{A} = 1 \text{ or } -1$.
   • proof $$\begin{array}{ll} \because & \text{Entries in } \boldsymbol{A} \text{ and } \boldsymbol{A}^{-1} \text{ are intergers.} \\ \therefore & \det \boldsymbol{A} \text{ and } \det \boldsymbol{A}^{-1} \text{ are also integers.} \\ \because & (\det \boldsymbol{A})(\det \boldsymbol{A}^{-1}) = (\det \boldsymbol{AA}^{-1}) = 1\\ \therefore & (\det \boldsymbol{A}) = (\det \boldsymbol{A}^{-1}) = \pm 1 \\ \end{array}$$
6. The cofactor matrix $\boldsymbol{C}$ of an orthogonal matrix $\boldsymbol{Q}$ will be also an orthogonal matrix.
   • proof $$\begin{array}{c} \boldsymbol{C} = (\det \boldsymbol{Q})(\boldsymbol{Q}^{-1})^{\text{T}} \\ \Downarrow \\ \text{When } \boldsymbol{Q} \text{ is orthonormal.} \\ \Downarrow \\ \boldsymbol{C} = \pm 1(\boldsymbol{Q}) \end{array}$$
7. If the columns of a $n$ by $n$ matrix have lengths $L_{1}, L_{2}, \cdots, L_{n}$, the largest possible value for the determinants is $\prod_{i=1}^{n}L_{i}$
   • When each columns are orthogonal the volumn of this matrix is largest.
8. When edge vectors $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$ are perpendicular,
   • $\boldsymbol{A}^{\text{T}}\boldsymbol{A} = \left[ \begin{matrix} \Vert \boldsymbol{a} \Vert & 0 & 0 \\ 0 & \Vert \boldsymbol{b} \Vert & 0 \\ 0 & 0 & \Vert \boldsymbol{c} \Vert \\ \end{matrix} \right]$
   • $\det {\boldsymbol{A}^{\text{T}}\boldsymbol{A}} = (\Vert \boldsymbol{a} \Vert \Vert \boldsymbol{b} \Vert \Vert \boldsymbol{c} \Vert)^{2}$
   • $\det {\boldsymbol{A}} = \Vert \boldsymbol{a} \Vert \Vert \boldsymbol{b} \Vert \Vert \boldsymbol{c} \Vert$
9. The volumn of pyramid in $\mathbb{R}^{\text{n}}$ is $\frac{1}{n!} \times \text{volumn of cube in } \mathbb{R}^{n}$
10. Cauchy-Binet formula: $$\begin{array}{c} \boldsymbol{AB} = \left[ \begin{matrix} a & b & c \\ d & e & f \end{matrix} \right] \left[ \begin{matrix} g & j \\ h & k \\ i & \ell \\ \end{matrix} \right] \\ (\det \boldsymbol{AB}) = \left\vert \begin{matrix} a & b \\ d & e \end{matrix} \right\vert \left\vert \begin{matrix} g & j \\ h & k \end{matrix} \right\vert + \left\vert \begin{matrix} a & c \\ d & f \end{matrix} \right\vert \left\vert \begin{matrix} g & i \\ i & \ell \end{matrix} \right\vert + \left\vert \begin{matrix} b & c \\ e & f \end{matrix} \right\vert \left\vert \begin{matrix} h & k \\ i & \ell \end{matrix} \right\vert \\ = \color{#D0104C}{\text{sum of (2 by 2 determinants in } \boldsymbol{A} \text{)(2 by 2 determinants in } \boldsymbol{B} \text{)}} \end{array}$$