Section02 Projections

Example

• What are the projections of $\boldsymbol{b} = (2,3,4)$ onto the $z$ axis and the $xy$ plane?
  • Projection onto $z$ axis:
    • $p_{z} = (0,0,4) = P_{z}\boldsymbol{b}$
    • $P_{z} = \left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{matrix} \right]$
  • Projection onto $xy$ plane
    • $p_{xy} = (2,3,0) = P_{xy}\boldsymbol{b}$
    • $P_{xy} = \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{matrix} \right]$

Goals and Descrption of Projection

Goals

• Find the part $p$ in each subspaces and the projection matrix $P$ that produces that part $p = P \boldsymbol{b}$. Every subspace of $\mathbb{R}^{m}$ has its own $m$ by $m$ projection matrix.

Description

• Project any $\boldsymbol{b}$ onto the column space of any $m$ by $n$ matrix.

Projection onto a line

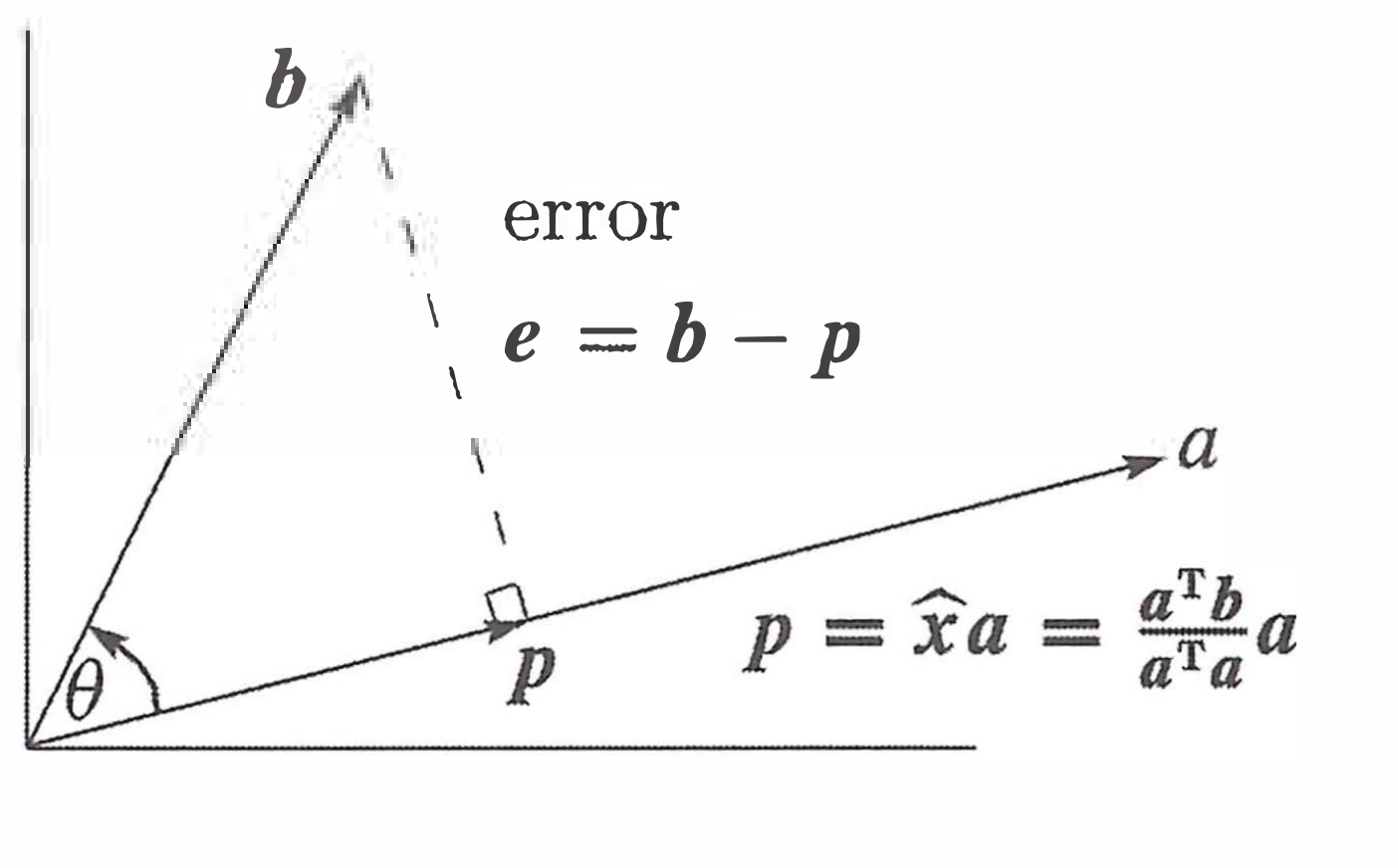
• As above picture, $\boldsymbol{b}$ is projected onto the line $\boldsymbol{a}$ on the point $\boldsymbol{p}$.
  • The point $\boldsymbol{p}$ is the point which is closest to $\boldsymbol{b}$.
  • The line $\boldsymbol{b} - \boldsymbol{p}$ is perpendicular to the line $\boldsymbol{a}$. Therefore, $\boldsymbol{a} \cdot (\boldsymbol{b} - \boldsymbol{p}) = 0$
  • Because the point $\boldsymbol{p}$ is on the line of $\boldsymbol{a}$, suppose $\boldsymbol{p} = \hat{x}\boldsymbol{a}$. ($\boldsymbol{p}$ is determined by $\hat{x}$)
  • $\boldsymbol{e} = \boldsymbol{b} - \boldsymbol{p} = \boldsymbol{b} - \hat{x} \boldsymbol{a}$
  • $\hat{x} = \frac{\boldsymbol{a} \cdot \boldsymbol{b}}{\boldsymbol{a} \cdot \boldsymbol{a}} = \frac{\boldsymbol{a}^{\text{T}}\boldsymbol{b}}{\boldsymbol{a}^{\text{T}}\boldsymbol{a}}$ (Compute from $\boldsymbol{a} \cdot \boldsymbol{e} = \boldsymbol{a}^{\text{T}}\boldsymbol{e} = 0$)
  • $\boldsymbol{p} = \boldsymbol{a} \hat{x} = \boldsymbol{a} \frac{\boldsymbol{a}^{\text{T}}\boldsymbol{b}}{\boldsymbol{a}^{\text{T}}\boldsymbol{a}} = \frac{\boldsymbol{aa}^{\text{T}}}{\boldsymbol{a}^{\text{T}}\boldsymbol{a}} \boldsymbol{b} = P \boldsymbol{b} \Rightarrow P = \frac{\boldsymbol{aa}^{\text{T}}}{\boldsymbol{a}^{\text{T}}\boldsymbol{a}}$

Steps of Projection

1. find $\hat{x}$
2. find the projection $\boldsymbol{p} = \boldsymbol{a} \hat{x}$
3. find the projection matrix $\boldsymbol{p} = \boldsymbol{Pb}$

Properties of Projection Matrix

1. $\color{#D0104C}{P^{2} = P}$ Projecting a second time doesn't change anything.
2. The diagonal entries of $P$ add up to 1. ($\sum_{i=1}^{n}{P_{ii}} = 1$)
3. $\boldsymbol{I} - P$ is the projection matrix, which projecting $\boldsymbol{b}$ to $\boldsymbol{e}$, which is perpendicular to $\boldsymbol{p}$.

Projection Onto a Subspace

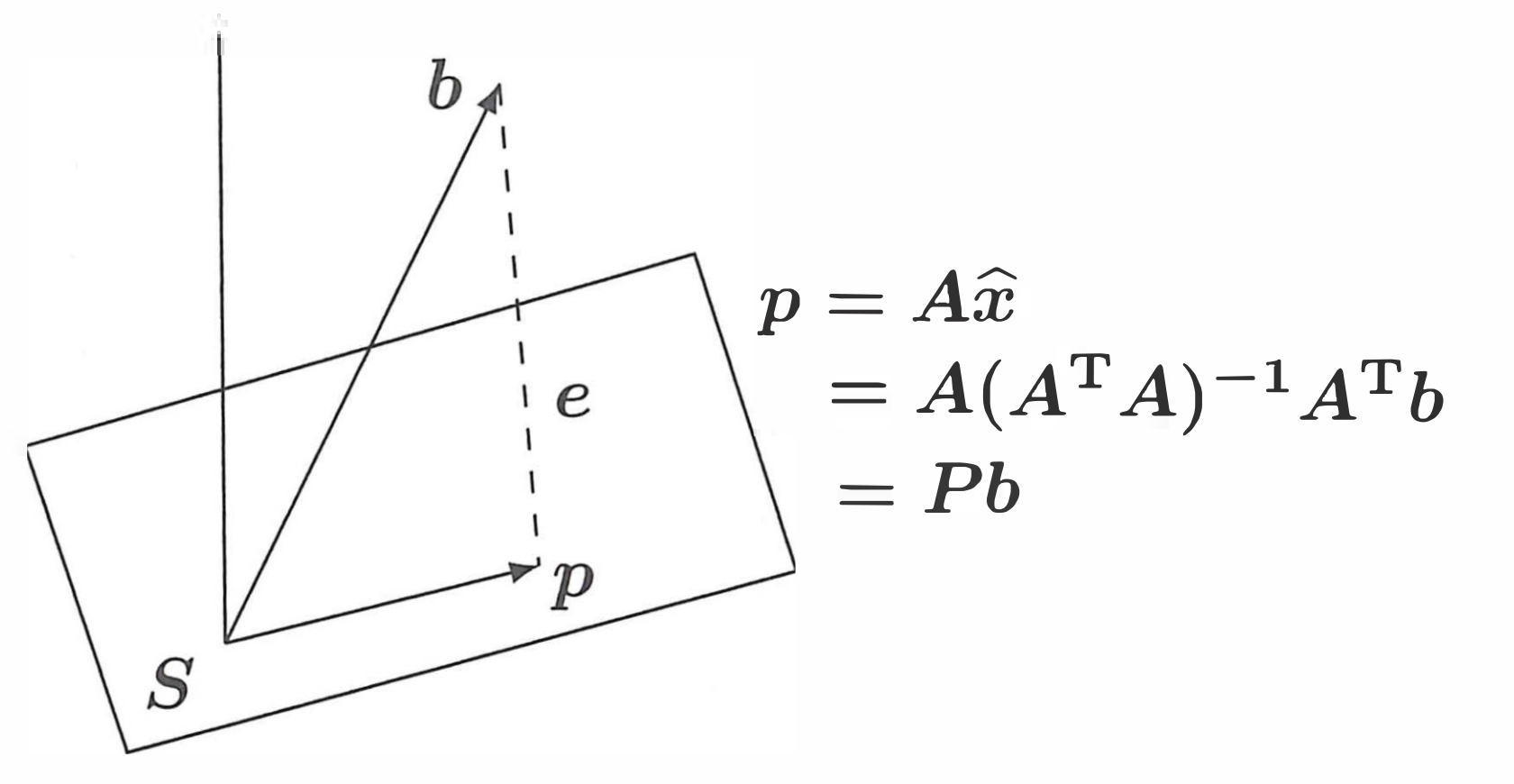
• Suppose the subspace $\boldsymbol{S}$ is the column space of $\boldsymbol{A}$, because $\boldsymbol{p} \in \boldsymbol{A}$, $\boldsymbol{p}$ is the linearly combination of $\boldsymbol{A}$'s columns, it could be denoted as $\boldsymbol{p} = \boldsymbol{A\hat{x}}$
• $\boldsymbol{A}^{\text{T}}\boldsymbol{e} = \boldsymbol{A}^{\text{T}}(\boldsymbol{b} - \boldsymbol{p}) = \boldsymbol{A}^{\text{T}}(\boldsymbol{b} - \boldsymbol{A \hat{x}}) = \boldsymbol{0}$
  • $\Rightarrow \boldsymbol{\hat{x}} = (\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1} \boldsymbol{A}^{\text{T}}\boldsymbol{b}$
  • $\Rightarrow \boldsymbol{p} = \boldsymbol{A\hat{x}} = \boldsymbol{A}(\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1} \boldsymbol{A}^{\text{T}}\boldsymbol{b}$
  • $\Rightarrow \boldsymbol{P} = \boldsymbol{A}(\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}\boldsymbol{A}^{\text{T}}$
• The $\boldsymbol{e} = \boldsymbol{b} - \boldsymbol{A \hat{x}}$ is contained in the nullspace of $\boldsymbol{A}^{\text{T}}$ (The left null space of $\boldsymbol{A}$)
• Because $\boldsymbol{A}$ is a rectangular matrix. $\boldsymbol{A}$ is not invertible. Therefore, $\boldsymbol{P} = \boldsymbol{A(\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1} \boldsymbol{A}^{\text{T}}} = \boldsymbol{AA}^{-1} (\boldsymbol{A}^{\text{T}})^{-1}\boldsymbol{A}^{\text{T}}$ is false. The $(\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}$ couldn't be split to $\boldsymbol{A}^{-1}(\boldsymbol{A}^{\text{T}})^{-1}$
• $\boldsymbol{A}^{\text{T}} \boldsymbol{A}$ is invertible, if and only if the columns of $\boldsymbol{A}$ are linearly independent.
• When $\boldsymbol{A}$ has independent columns, $\boldsymbol{A}^{\text{T}}\boldsymbol{A}$ is square, symmetric, and invertible.

Properties from Exercises

1. We can add projections onto orthogonal vectors to get the projection matrix onto the larger space.
   • When we projecting a vector onto vectors which are not orthogonal, the sum of projections is not equal to the ortiginal vector.
2. $(\boldsymbol{I} - \boldsymbol{P})^{2} = \boldsymbol{I} - \boldsymbol{P}$
   • Proof $$(\boldsymbol{I} - \boldsymbol{P})^{2} = \boldsymbol{I}^{2} + \boldsymbol{P}^{2} - \boldsymbol{PI} - \boldsymbol{IP} = \boldsymbol{I} + \boldsymbol{P} - 2 \boldsymbol{P} = \boldsymbol{I} - \boldsymbol{P}$$
3. If $\boldsymbol{A}$ is invertible, the column space of $\boldsymbol{A}$ is all $\mathbb{R}^{n}$, $\boldsymbol{e} = 0$
4. The column of $\boldsymbol{P}$ is the space that $\boldsymbol{P}$ projects onto.
5. $\boldsymbol{A}^{\text{T}}\boldsymbol{Ax} = \boldsymbol{0} \Rightarrow \boldsymbol{Ax} = \boldsymbol{0}$
   • proof $$\begin{array}{ll} \because & \boldsymbol{A}^{\text{T}}\boldsymbol{Ax} = \boldsymbol{0} \\ \therefore & \boldsymbol{Ax} \text{ is in the left nullsapce of } \boldsymbol{A} \text{ and } \boldsymbol{Ax} \text{ is in the column space of } \boldsymbol{A}\\ \because & \text{the column space and the left nullspace are orthogonal.} \\ \therefore & (\boldsymbol{Ax}) \cdot \boldsymbol{Ax} = (\boldsymbol{Ax})^{\text{T}}\boldsymbol{Ax} = \boldsymbol{0} \\ \therefore & \boldsymbol{Ax} = \boldsymbol{0} \\ \end{array}$$