Section03 Least Squares Approximations

• When $\boldsymbol{Ax} = \boldsymbol{b}$ has no solutions, multiply by $\boldsymbol{A}^{\text{T}}$ and solve $\boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b}$

Minimizing the Error

By geometry

• Find the line which through $\boldsymbol{b}$ and is perpendicular to the coloumn space of $\boldsymbol{A}$, the intersectional point between this line and the column space of $\boldsymbol{A}$ is the point which is nearest to $\boldsymbol{b}$ in the column space of $\boldsymbol{A}$.

By algebra

• Every vector $\boldsymbol{b}$ could be split into two parts:

  • $\boldsymbol{b} = \boldsymbol{p} + \boldsymbol{e}; \left\{ \begin{array}{ll} \boldsymbol{p} & \text{the part in the column space of } \boldsymbol{A}.\\ \boldsymbol{e} & \text{the part is perpendicular to the column space.} \end{array} \right.$

• Because $\boldsymbol{p}$ is contained in the column space of $\boldsymbol{A}$, It is always solvable to $\boldsymbol{A \hat{x}} = \boldsymbol{p}$.

• Squared length for any $\boldsymbol{x}$
  • $\Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2} = \Vert \boldsymbol{Ax} - \boldsymbol{p} \Vert^{2} + \Vert \boldsymbol{e} \Vert^{2}$
  • proof $$\begin{array}{ll} \because & \Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2} = (\boldsymbol{Ax} - \boldsymbol{b})^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{b}) \text{ and } \boldsymbol{b} = \boldsymbol{p} + \boldsymbol{e} \\ \therefore & \Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2} = (\boldsymbol{Ax} - \boldsymbol{p} - \boldsymbol{e})^{\text{T}} (\boldsymbol{Ax} - \boldsymbol{p} - \boldsymbol{e}) \\ & = (\boldsymbol{Ax} - \boldsymbol{p})^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{p}) + \boldsymbol{e}^{\text{T}} - (\boldsymbol{Ax} - \boldsymbol{p})^{\text{T}}\boldsymbol{e} - \boldsymbol{e}^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{p})\\ \because & \boldsymbol{e} \text{ is perpendicular to the column space of } \boldsymbol{A} \\ & \text{and } \boldsymbol{p} \text{ is contained in the column space of } \boldsymbol{A} \\ \therefore & (\boldsymbol{Ax} - \boldsymbol{p})^{\text{T}} \boldsymbol{e} = \boldsymbol{e}^{\text{T}} (\boldsymbol{Ax} - \boldsymbol{p}) = 0 \\ \therefore & \Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2} = (\boldsymbol{Ax} - \boldsymbol{p})^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{p}) + \boldsymbol{e}^{\text{T}} \boldsymbol{e} \\ & = \Vert \boldsymbol{Ax} - \boldsymbol{p} \Vert^{2} + \Vert \boldsymbol{e} \Vert^{2} \end{array}$$

By calculus

• The partial derivatives of $\Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2}$ are zero when $\boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b}$
  • proof $$\begin{array}{ll} & \text{Suppose } f(\boldsymbol{x}) = \Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2} \\ \because & \Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert^{2} = (\boldsymbol{Ax} - \boldsymbol{b})^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{b}) \\ \therefore & \frac{\partial{f}}{\partial{\boldsymbol{x}}} = \boldsymbol{A}^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{b}) + (\boldsymbol{Ax} - \boldsymbol{b})^{\text{T}}\boldsymbol{A} \\ \because & \boldsymbol{A}^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{b}) = (\boldsymbol{Ax} - \boldsymbol{b})^{\text{T}}\boldsymbol{A} = (\boldsymbol{Ax} - \boldsymbol{b}) \cdot \boldsymbol{A} \\ \therefore & \frac{\partial{f}}{\partial{\boldsymbol{x}}} = 2 \boldsymbol{A}^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{b}) \\ \because & \frac{\partial{f}}{\partial{\boldsymbol{x}}} = \boldsymbol{0} \\ \therefore & \boldsymbol{A}^{\text{T}}(\boldsymbol{Ax} - \boldsymbol{b}) = \boldsymbol{0} \\ \therefore & \boldsymbol{A}^{\text{T}}\boldsymbol{Ax} = \boldsymbol{A}^{\text{T}} \boldsymbol{b} \\ \end{array}$$

The Big Picture for Least Squares

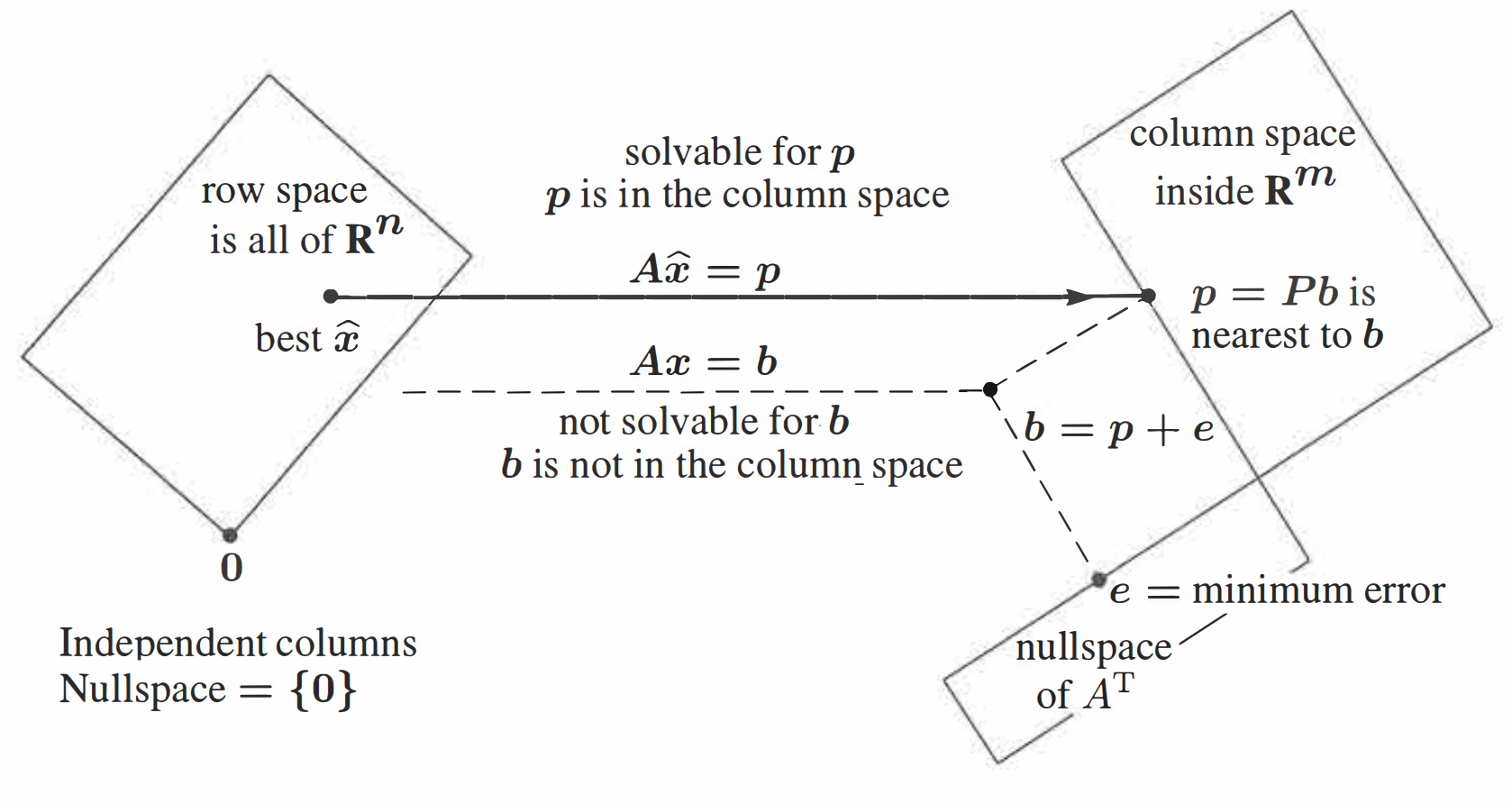
• The row space of $\boldsymbol{A}$ is the all $\mathbb{R}^{n}$. (Because matrix $\boldsymbol{A}$ is a column full rank matrix.)
• The $\boldsymbol{b}$ is a point which is not contained in the column space of $\boldsymbol{A}$
• The $\boldsymbol{b}$ could be split into two parts:
  1. The part $\boldsymbol{p}$ which is contained in the column space of $\boldsymbol{A}$.
  2. The part $\boldsymbol{e}$ which is orthogonal to the column space of $\boldsymbol{A}$ (The nullspace of $\boldsymbol{A}^{\text{T}}$)

Fitting a Straight Line

One Factor

• $\boldsymbol{Ax} = \boldsymbol{b}$ is $\begin{array}{c} C + Dt_{1} = b_{1} \\ C + Dt_{2} = b_{2} \\ \vdots \\ C + Dt_{m} = b_{m} \end{array}$ with $\boldsymbol{A} = \left[ \begin{matrix} 1 & t_{1} \\ 1 & t_{2} \\ \vdots & \vdots\\ 1 & t_{m} \end{matrix} \right]$
• Slove $\boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b}$ for $\boldsymbol{\hat{x}} = (C,D)$. The errors are $e_{i} = b_{i} - C - Dt_{i}$

• Computation

  • $\boldsymbol{A}^{\text{T}}\boldsymbol{A} = \left[ \begin{matrix} 1 & \cdots & 1 \\ t_{1} & \cdots & t_{m} \end{matrix} \right] \left[ \begin{matrix} 1 & t_{1} \\ \vdots & \vdots \\ 1 & t_{m} \end{matrix} \right] = \left[ \begin{matrix} m & \sum_{i=1}^{m}{t_{i}} \\ \sum_{i=1}^{m}{t_{i}} & \sum_{i=1}^{m}{t_{i}^{2}} \end{matrix} \right]$
  • $\boldsymbol{A}^{\text{T}}\boldsymbol{b} = \left[ \begin{matrix} 1 & \cdots & 1 \\ t_{1} & \cdots & t_{m} \\ \end{matrix} \right] \left[ \begin{matrix} b_{1} \\ \vdots \\ b_{m} \end{matrix} \right] = \left[ \begin{matrix} \sum_{i=1}^{m}{b_{i}} \\ \sum_{i=1}^{m}{t_{i}b_{i}} \end{matrix} \right]$
  • $\boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b} \Rightarrow \left[ \begin{matrix} m & \sum_{i=1}^{m}{t_{i}} \\ \sum_{i=1}^{m}{t_{i}} & \sum_{i=1}^{n}{t_{i}^{2}} \end{matrix} \right] \left[ \begin{matrix} C \\ D \end{matrix} \right] = \left[ \begin{matrix} \sum_{i=1}^{m}{b_{i}} \\ \sum_{i=1}^{m}{t_{i}b_{i}} \end{matrix} \right]$

• The Derivatieve of Squares is linear.

• Then the columns of $\boldsymbol{A}$ are perpendicular to each other, the result of $\boldsymbol{A}^{\text{T}}\boldsymbol{A}$ is a diagonal matric, it's easier to solve the equation $\boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b}$ (Gram-Schemidt idea)

Dependent Columns in $\boldsymbol{A}$: What is $\boldsymbol{\hat{x}}$?

• Example
  • $\boldsymbol{A} = \left[ \begin{matrix} 1 & 1 \\ 1 & 1 \end{matrix} \right]; \boldsymbol{b} = \left[ \begin{matrix} 1 \\ 3 \end{matrix} \right]$
  • $\Rightarrow \boldsymbol{A \hat{x}} = \left[ \begin{matrix} 2 \\ 2 \end{matrix} \right] = \boldsymbol{p}$ These equations have infinite solutions($\boldsymbol{\hat{x}}$).

Fitting by a Parabola

Nonlinearly Problem

• Even with a nonlinear funcaiton like $C + Dt + Et^{2}$, the unknown $C, D, E$ still apear linearly!

Properties from Exercises

1. Least sum($\sum_{i=1}^{m}{\vert e_{i} \vert}$) come from the median measurements. It is not influenced by outliers as heavily as LSQ.
2. If multply $\boldsymbol{b}$ by $M$ and then add $N$ to get $\boldsymbol{b}_{\text{new}}$, the solution of $C + Ex = b$:
   • $C_{\text{new}} = MC + N$
   • $E_{\text{new}} = ME$
3. The $\bar{t}$ and $\bar{b}$ is on the least squares approximated line.
   • proof $$\begin{array}{ll} & \text{Suppose } \boldsymbol{A} = \left[ \begin{matrix} 1 & t_{11} & t_{12} & \cdots & t_{1n} \\ 1 & t_{21} & t_{22} & \cdots & t_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & t_{m1} & t_{m2} & \cdots & t_{mn} \end{matrix} \right], \boldsymbol{b} = \left[ \begin{matrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \end{matrix} \right]\\ \therefore & \boldsymbol{A}^{\text{T}} = \left[ \begin{matrix} 1 & 1 & \cdots & 1 \\ t_{11} & t_{21} & \cdots & t_{m1} \\ t_{12} & t_{22} & \cdots & t_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ t_{1n} & t_{2n} & \cdots & t_{mn} \\ \end{matrix} \right]\\ \because & \text{The least squares approximatation is the solution to } \boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b} \\ \because & \boldsymbol{A}^{\text{T}}\boldsymbol{A} = \left[ \begin{matrix} m & \sum_{i=1}^{m}t_{i1} & \sum_{i=1}^{m}t_{i2} & \cdots & \sum_{i=1}^{m}t_{in} \\ \vdots & \vdots & \vdots & \vdots & \vdots \end{matrix} \right] \\ & \boldsymbol{A}^{\text{T}}\boldsymbol{b} = \left[ \begin{matrix} \sum_{i=1}^{m}{b_{i}} \\ \vdots \end{matrix} \right] \\ \therefore & \text{The first equation is } m \hat{x}_{0} + \sum_{i=1}^{m}t_{i1} \hat{x}_{1} + \sum_{i=1}^{m}{t_{i2}} \hat{x}_{2} + \sum_{i=1}^{m}{t_{in}} \hat{x}_{n} = \sum_{i=1}^{m}{b_{i}} \\ \therefore & \hat{x}_{0} + \bar{t}_{\boldsymbol{\cdot}1}\hat{x}_{1} + \bar{t}_{\boldsymbol{\cdot}2}\hat{x}_{2} + \cdots + \bar{t}_{\boldsymbol{\cdot}n}\hat{x}_{n} = \bar{b}\\ \end{array}$$
4. When $\boldsymbol{A} = \left[ \begin{matrix} 1 \\ 1 \\ \vdots \\ 1 \end{matrix} \right]$ the solution to $\boldsymbol{A}^{\text{T}}\boldsymbol{A \hat{x}} = \boldsymbol{A}^{\text{T}}\boldsymbol{b}$ is the mean of $\boldsymbol{b}$ ($\hat{x} = \bar{\boldsymbol{b}}$).
5. $\boldsymbol{\hat{x}}$ is the unbiased estimate of $\boldsymbol{x}$
   • proof $$\begin{array}{ll} \boldsymbol{e} = \boldsymbol{b} - \boldsymbol{Ax} \\ \Rightarrow (\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}\boldsymbol{A}^{\text{T}} \boldsymbol{e} = (\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}\boldsymbol{A}^{\text{T}} \boldsymbol{b} - (\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}\boldsymbol{A}^{\text{T}} \boldsymbol{Ax} \\ \Rightarrow (\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}\boldsymbol{0} = \boldsymbol{\hat{x}} - \boldsymbol{Ix} \\ \Rightarrow \boldsymbol{0} = \boldsymbol{\hat{x}} -\boldsymbol{x} \end{array}$$
6. The $m$ errors $e_{i}$ are independent with variance $\sigma^{2}$ ($\boldsymbol{ee}^{\text{T}} = (\boldsymbol{b} - \boldsymbol{Ax})(\boldsymbol{b} - \boldsymbol{Ax})^{\text{T}} = \sigma^{2}\boldsymbol{I}$) $\Rightarrow (\boldsymbol{\hat{x}} - \boldsymbol{x})(\boldsymbol{\hat{x}} - \boldsymbol{x})^{\text{T}} = \sigma^{2}(\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}$
7. $\boldsymbol{e}$ is contained in the left nullspace of $\boldsymbol{A}$ ($\boldsymbol{N}(\boldsymbol{A}^{\text{T}})$), $\boldsymbol{p}$ is contained in the columns space of $\boldsymbol{A}$ ($\boldsymbol{C}(\boldsymbol{A})$), $\boldsymbol{\hat{x}}$ is contained in the row space of $\boldsymbol{A}$ ($\boldsymbol{C}(\boldsymbol{A}^{\text{T}})$)
8. If $\boldsymbol{A}$ has dependent columns, then $\boldsymbol{A}^{\text{T}}\boldsymbol{A}$ is not invertible and the usual formula $\boldsymbol{P} = \boldsymbol{A}(\boldsymbol{A}^{\text{T}}\boldsymbol{A})^{-1}\boldsymbol{A}^{\text{T}}$ will fail. Replace $\boldsymbol{A}$ in that formula by the matrix $\boldsymbol{B}$ that keeps only the pivot columns of $\boldsymbol{A}$.