Section01 Orthogonality of the Four Subspaces

Defination

Orthogonal Vectors

• If the result of two vectors' dot multiplication is equal to 0, then these two vectors are orthogonal. $$\begin{array}{c} \boldsymbol{v} \text{ and } \boldsymbol{w} \text{ are orthogonal.} \\ \Downarrow \\ \boldsymbol{v} \cdot \boldsymbol{w} = 0 \\ \Downarrow \\ \boldsymbol{v}^{\text{T}}\boldsymbol{w} = 0 \\ \Vert \boldsymbol{v} + \boldsymbol{w} \Vert^{2} = \Vert \boldsymbol{v} \Vert^{2} + \Vert \boldsymbol{w} \Vert^{2} \end{array}$$

Orthogonal Subspaces

• Two subspaces $\boldsymbol{V}$ and $\boldsymbol{W}$ are orthogonal if every vector $\boldsymbol{v}$ in $\boldsymbol{V}$ is perpendicular to every vector $\boldsymbol{w}$ in $\boldsymbol{W}$. $$\begin{array}{c} \boldsymbol{v}^{\text{T}}\boldsymbol{w} = 0 \text{ for all } \boldsymbol{v} \text{ in } \boldsymbol{V} \text{ and all } \boldsymbol{w} \text{ in } \boldsymbol{W} \end{array}$$

Some Properties of Orthogonal

• Two planes (Dimension 2 and 2 in $\mathbb{R}^{3}$) can't be orthogonal subspaces. (The intersection of them is not perpendicular to themselves.)
• When a vector is in two orthogonal subspaces, it must to be zeros. It is perpendicular to itself.

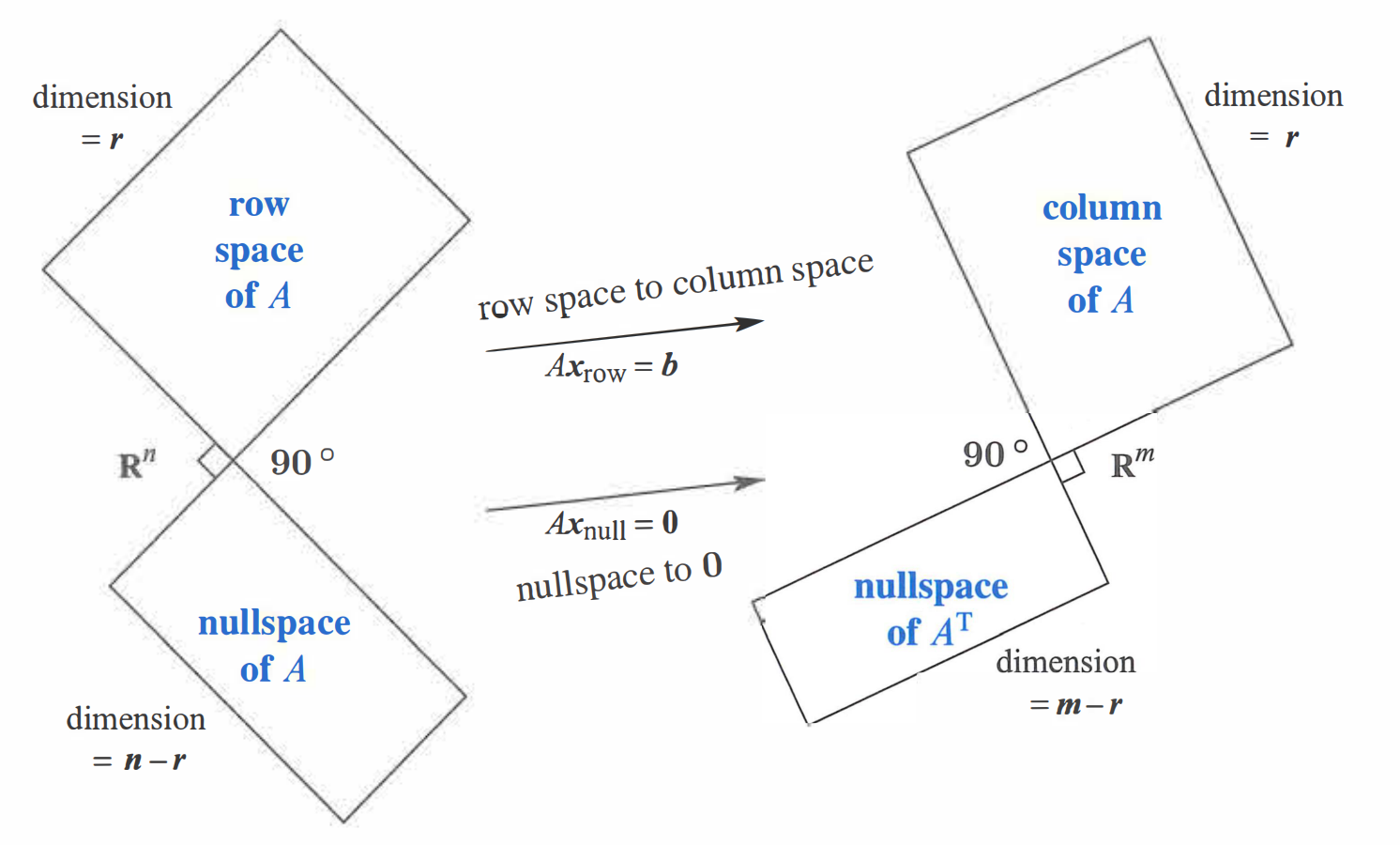
Orthogonality of the Four Subspaces

Row space and Nullspace

• Every vector $\boldsymbol{x}$ in the nullspace is perpendicular to every row of $\boldsymbol{A}$, because $\boldsymbol{Ax} = \boldsymbol{0}$. The nullspace $\boldsymbol{N}(\boldsymbol{A})$ and the row space $\boldsymbol{C}(\boldsymbol{A}^{\text{T}})$ are orthogonal subspaces of $\mathbb{R}^{n}$.

Column space ang Left Nullspace

• Every vector $\boldsymbol{y}$ in the nullspace of $\boldsymbol{A}^{\text{T}}$ is permendicular to every column of $\boldsymbol{A}$. The left nullspace $\boldsymbol{N}(\boldsymbol{A}^{\text{T}})$ and the column space $\boldsymbol{C}(\boldsymbol{A})$ are orthogonal in $\mathbb{R}^{m}$.

Orthogonal Complements

Defination

• The orthogonal complements of a subspace $\boldsymbol{V}$ contains every vectors that is perpendicular to $\boldsymbol{V}$. This orthogonal subspace is denoted by $\boldsymbol{V}^{\perp}$

Fundamental Subspaces

• $\boldsymbol{N}(\boldsymbol{A})$ is the orthogonal complement of the row space $\boldsymbol{C}(\boldsymbol{A}^{\text{T}})$(in $\mathbb{R}^{n}$)
• $\boldsymbol{N}(\boldsymbol{A}^{\text{T}})$ is the orthogonal complement of the column space $\boldsymbol{C}(\boldsymbol{A})$(in $\mathbb{R}^{m}$)

Properties

• If $\boldsymbol{v}$ is orthogonal to the nullspace, it must be in the row space.
  • If $\boldsymbol{v}$ is not in the row space, it could be add to the row space as an extra row, which breaks $r + (n-r) = n$.
• The only vector in two orthogonal subpsace is the zero vector.
• Inside $\mathbb{R}^{n}$, the dimension of complements $\boldsymbol{V}$ and $\boldsymbol{W}$ add to $n$.

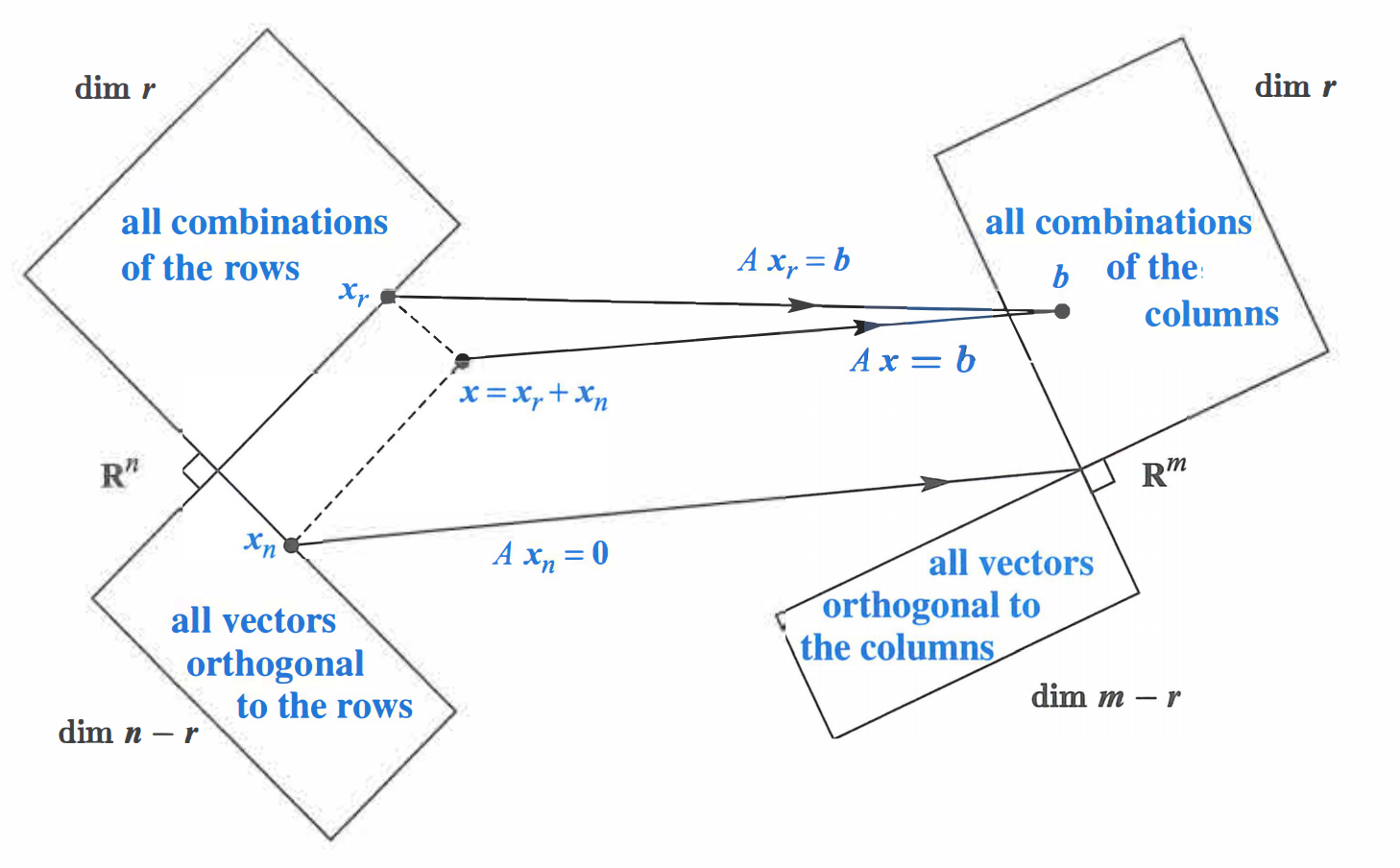
Split

• every $\boldsymbol{x}$ could be split into a row space component $\boldsymbol{x}_{r}$ and a nullspace component $\boldsymbol{x}_{n}$ $$\begin{array}{c} \boldsymbol{x} = \boldsymbol{x}_{n} + \boldsymbol{x}_{r} \\ \Downarrow \\ \boldsymbol{Ax} = \boldsymbol{Ax}_{n} + \boldsymbol{Ax}_{r} \end{array}$$

Row space 2 Column space

Combining Bases from Subspaces

Basis

• Any $n$ independent vectors in $\mathbb{R}^{n}$ must span $\mathbb{R}^{n}$. So they are a basis.
• Any $n$ vectors that span $\mathbb{R}^{n}$ must be independent. So they are a basis.

Number of solutions

• If the $n$ columns of $\boldsymbol{A}$ are independent, they span $\mathbb{R}^{n}$. So $\boldsymbol{Ax} = \boldsymbol{b}$ is solvable.
• If the $n$ columns span $\mathbb{R}^{n}$, they are independent. So $\boldsymbol{Ax} = \boldsymbol{b}$ has only one solution.

Properties from Exercises

1. Fredholm's Alternative $\boldsymbol{Ax} = \boldsymbol{b}; \boldsymbol{A}^{\text{T}}\boldsymbol{y} = 0 \text{ with } \boldsymbol{y}^{\text{T}} \boldsymbol{b} \ne 0$
   • meaning: $$\begin{array}{ll} \because & \boldsymbol{b} \nsubseteq \boldsymbol{C}(\boldsymbol{A}) \\ \therefore & \boldsymbol{b} \text{ is not orthogonal to the left nullspace.}(\boldsymbol{y}^{\text{T}}\boldsymbol{b} \ne 0) \\ \end{array}$$
2. If $\boldsymbol{A}^{\text{T}} \boldsymbol{Ax} = \boldsymbol{0}$, then $\boldsymbol{Ax} = 0 \Rightarrow$ $\boldsymbol{A}^{\text{T}}\boldsymbol{A}$ has the same nullspace as $\boldsymbol{A}$.
3. $\boldsymbol{S} \subseteq \boldsymbol{V} \Rightarrow \boldsymbol{S^{\perp}} \supseteq \boldsymbol{V}^{\perp}$
4. The nullspace of (nullspace of $\boldsymbol{A}$) is the Row space of $\boldsymbol{A}$.